Đề thi học sinh giỏi cấp tỉnh Môn Toán lớp 12 năm học 2022 – 2023 sở GD&ĐT Phú Thọ có đáp án và giải chi tiết

Đề thi này bám sát theo chương trình học và thi TN THPT nên các em dùng để ôn luyện thoải mái nhé.

Đề gồm hai phần: phần tự luận gồm 04 câu (08 điểm), phần trắc nghiệm gồm 40 câu (12 điểm), thời gian làm bài 180 phút. Phần thi trắc nghiệm có một số câu hỏi khó khá hay.

Một số câu hỏi có trong đề thi này:

+ Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = x3 – (m + 1)x + 4 − m cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn -3. Cho x, y là hai số thực dương, tìm giá trị lớn nhất của biểu thức P.
+ Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 2a, AD = 2a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M là trung điểm cạnh AD. Tính khoảng cách từ điểm B đến mặt phẳng (SCM). Cho hình lăng trụ ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật, AB = 6, AD = 3, A’C = 3 và mặt phẳng (ACC’A’) vuông góc với mặt phẳng đáy. Biết góc giữa hai mặt phẳng (ACC’A’) và (ADD’A’) là a thỏa mãn tana = 3/2. Tính thể tích của khối lăng trụ ABCD.A’B’C’D’.
+ Hai bạn Quý và Mão mỗi bạn chọn ngẫu nhiên một tập con khác rỗng từ tập E = {1; 2; 3; 4; 5; 6; 7; 8; 9}. Tính xác suất để mỗi bạn chọn được một tập con có 3 phần tử và trong hai tập con đó có ít nhất hai phần tử giống nhau.

Câu 29. Cho hàm số $f\left( x \right)$ thỏa mãn $f\left( 1 \right)=\ln 4$ và ${f}'\left( x \right)=\dfrac{f\left( x \right)+x+1}{x+1}$ với mọi $x>0.$ Giá trị của $f\left( 3 \right)$ bằng

Câu 30. Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác cân tại $A,\text{ }SA$ vuông góc với mặt phẳng $\left( ABC \right).$ Gọi $M$ là trung điểm của cạnh $BC.$ Cạnh bên $SB$ lần lượt tạo với mặt phẳng đáy và mặt phẳng $\left( SAM \right)$ các góc bằng ${{30}^{0}}$ và ${{45}^{0}},$ khoảng cách từ $S$ đến cạnh $BC$ bằng $a.$ Thể tích của khối chóp $S.ABC$ bằng

Câu 31. Số giá trị nguyên của tham số $a$ thuộc khoảng $\left( 1;+\infty \right)$ để \[\int\limits_{0}^{\dfrac{\pi }{4}}{{{\log }_{a}}\left( 1+\tan x \right)dx}\ge \dfrac{\pi }{16}\] là

Câu 35. Cho tham số $m>1,$ biết đồ thị hàm số $y={{x}^{4}}+{{x}^{3}}-1+m$ cắt đường thẳng $y=x+m$ tại hai điểm phân biệt $A$ và $B$ sao cho $\tan \widehat{AOB}=-3$ (với $O$ là gốc tọa độ). Mệnh đề nào dưới đây đúng?

Câu 36. Cho hàm số \[f\left( x \right)=a{{x}^{4}}+b{{x}^{3}}+{{x}^{2}}-3\] với $a,\text{ }b$ là hai số nguyên dương và $a<4.$ Có bao nhiêu cặp số $\left( a;b \right)$ để hàm số $f\left( x \right)$ đạt giá trị nhỏ nhất tại $x=0?$

Câu 37. Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình thang vuông tại $A$ và $D\text{ }\left( CD<AB \right),$ cạnh bên $SC=\sqrt{5}a.$ Tam giác $SAD$ đều cạnh $2a$ và nằm trong mặt phẳng vuông góc với mặt phẳng $\left( ABCD \right).$ Gọi $H,\text{ }K$ lần lượt là trung điểm của cạnh $AD$ và $AB,$ khoảng cách từ $B$ tới mặt phẳng $\left( SHC \right)$ bằng $\dfrac{5\sqrt{2}a}{2}.$ Bán kính của mặt cầu đi qua bốn điểm $S,\text{ }B,\text{ }C,\text{ }K$ bằng

Câu 38. Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ. Biết $f\left( a \right)=1,\text{ }f\left( b \right)=9.$

Tập hợp tất cả các giá trị của tham số $m$ để phương trình $\log _{3}^{2}f\left( x \right)-2{{\log }_{3}}f\left( x \right)-m=0$ có $8$ nghiệm phân biệt là

Câu 39. Cho hàm số $f\left( x \right)$ có đạo hàm cấp $3$ trên $\mathbb{R}$ và thỏa mãn $f\left( 1-x \right)=x\left[ 2023-x{f}''\left( x \right) \right]$ với mọi $x\in \mathbb{R}.$ Tích phân $\int\limits_{0}^{1}{x{f}'\left( x \right)}dx$ bằng

Câu 40. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh $a,\text{ }\widehat{ABC}={{60}^{0}}.$ Tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy. Gọi $E,\text{ }F,\text{ }G,\text{ }H,\text{ }I,\text{ }K$ lần lượt là trung điểm các đoạn thẳng $AB,\text{ }BC,\text{ }CD,\text{ }DA,\text{ }SB$ và $SC.$ Thể tích của khối đa diện $IKEFGH$ bằng

Xem trực tiếp và tải đề thi về (Bản đẹp của đề thi kèm đáp án và lời giải chi tiết sẽ được Vted cập nhật trong thời gian sớm nhất)

ĐÁP ÁN

Câu 1.1. Tìm tất cả các giá trị thực của tham số $m$ để đồ thị hàm số $y={{x}^{3}}-\left( m+1 \right)x+4-m$ cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn $-3.$

Giải. Xét ${{x}^{3}}-\left( m+1 \right)x+4-m=0\Leftrightarrow m\left( x+1 \right)={{x}^{3}}-x+4\Leftrightarrow m=g\left( x \right)=\dfrac{{{x}^{3}}-x+4}{x+1},\left( x\ne -1 \right)$

Ta có ${g}'\left( x \right)=\dfrac{\left( 3{{x}^{2}}-1 \right)\left( x+1 \right)-1\left( {{x}^{3}}-x+4 \right)}{{{\left( x+1 \right)}^{2}}}=\dfrac{2{{x}^{3}}+3{{x}^{2}}-5}{{{\left( x+1 \right)}^{2}}}\Rightarrow {g}'\left( x \right)=0\Leftrightarrow x=1$

Bảng biến thiên trên $\left( -3;+\infty \right)\backslash \left\{ -1 \right\}$ như sau:

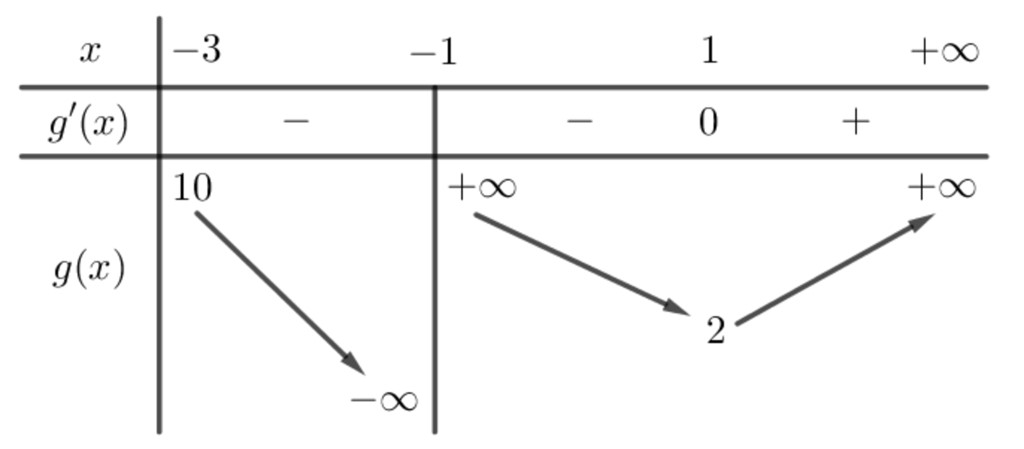
Vậy $2<m<10$ là giá trị cần tìm.

Câu 1.2. Cho hai số thực dương $x,y.$ Tìm giá trị lớn nhất của biểu thức $P=\dfrac{y}{{{x}^{2}}y+1}-\dfrac{2+{{y}^{3}}}{{{\left( x+y \right)}^{2}}}-\dfrac{128}{729}\left( x+y \right).$

Giải. Ta có $P=\dfrac{y}{{{x}^{2}}y+1}-\dfrac{{{y}^{3}}}{{{\left( x+y \right)}^{2}}}-\left[ \dfrac{2}{{{\left( x+y \right)}^{2}}}+\dfrac{128}{729}\left( x+y \right) \right]$ vì vậy ta sẽ tìm cách đánh giá $\dfrac{y}{{{x}^{2}}y+1}-\dfrac{{{y}^{3}}}{{{\left( x+y \right)}^{2}}}$ theo $\left( x+y \right)$

Theo bất đẳng thức Cauchy – Schwarz ta có:

$\left( {{y}^{3}}+1 \right)\left( 1+{{x}^{2}}y \right)\ge {{\left( \sqrt{{{y}^{3}}}+\sqrt{{{x}^{2}}y} \right)}^{2}}=y{{\left( x+y \right)}^{2}}\Rightarrow \dfrac{y}{{{x}^{2}}y+1}\le \dfrac{{{y}^{3}}+1}{{{\left( x+y \right)}^{2}}}$

Vì vậy \[P\le -\dfrac{1}{{{\left( x+y \right)}^{2}}}-\dfrac{128}{729}\left( x+y \right)=-\left( \dfrac{1}{{{t}^{2}}}+\dfrac{128}{729}t \right),\left( t=x+y>0 \right)\]

\[=-\left( \dfrac{1}{{{t}^{2}}}+\dfrac{64}{729}t+\dfrac{64}{729}t \right)\le -3\sqrt[3]{\dfrac{1}{{{t}^{2}}}.\dfrac{64}{729}t.\dfrac{64}{729}t}=-\dfrac{16}{27}.\]

Vậy ${{P}_{\max }}=-\dfrac{16}{27}$ dấu bằng xảy ra khi $\dfrac{1}{{{t}^{2}}}=\dfrac{64}{729}t\Leftrightarrow t=x+y=\dfrac{9}{4}$ và $\dfrac{\sqrt{{{y}^{3}}}}{1}=\dfrac{1}{\sqrt{{{x}^{2}}y}}$ chẳng hạn $x=\dfrac{1}{4};y=2.$

Câu 2. Giải phương trình ${{3}^{x-3+\sqrt[3]{7-3x}}}+\left( {{x}^{3}}-9{{x}^{2}}+24x+7 \right){{.3}^{x-3}}={{3}^{x}}+1$

Giải. Chia cả hai vế phương trình cho ${{3}^{x-3}}$ ta được: ${{3}^{\sqrt[3]{7-3x}}}+{{x}^{3}}-9{{x}^{2}}+24x+7=27+{{3}^{3-x}}$

$\Leftrightarrow {{3}^{\sqrt[3]{7-3x}}}+7-3x={{3}^{3-x}}+{{\left( 3-x \right)}^{3}}\Leftrightarrow \sqrt[3]{7-3x}=3-x$ do hàm số $g\left( t \right)={{3}^{t}}+{{t}^{3}}$ đồng biến trên $\mathbb{R}$

Vậy ${{\left( 3-x \right)}^{3}}=7-3x\Leftrightarrow {{x}^{3}}-9{{x}^{2}}+24x-20=0\Leftrightarrow x=2;x=5.$

Câu 3.1. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB=2a,\text{ }AD=\sqrt{2}a.$ Tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy. Gọi $M$ là trung điểm cạnh $AD.$ Tính khoảng cách từ điểm $B$ đến mặt phẳng $\left( SCM \right).$

Câu 3.2. Cho hình lăng trụ $ABCD.{A}'{B}'{C}'{D}'$ có đáy $ABCD$ là hình chữ nhật, $AB=\sqrt{6},\text{ }AD=\sqrt{3},\text{ }{A}'C=3$ và mặt phẳng $\left( AC{C}'{A}' \right)$ vuông góc với mặt phẳng đáy. Biết góc giữa hai mặt phẳng $\left( AC{C}'{A}' \right)$ và $\left( AD{D}'{A}' \right)$ là $\alpha $ thỏa mãn $\tan \alpha =\dfrac{3}{2}.$ Tính thể tích của khối lăng trụ $ABCD.{A}'{B}'{C}'{D}'.$

Câu 4. Hai bạn Quý và Mão mỗi bạn chọn ngẫu nhiên một tập con khác rỗng từ tập $E=\left\{ 1;2;3;4;5;6;7;8;9 \right\}.$ Tính xác suất để mỗi bạn chọn một tập con có $3$ phần tử và trong hai tập con đó có ít nhất hai phần tử giống nhau.

Giải. Tập $E=\left\{ 1,2,3,4,5,6,7,8,9 \right\}$ gồm 9 phần tử nên số tập con khác rỗng của $E$ là ${{2}^{9}}-1=511.$

Mỗi bạn có 511 cách chọn ngẫu nhiên nên $n\left( \Omega \right)={{511}^{2}}.$ Gọi $A$ là biến cố cần tính xác suất.

TH1: Hai tập con các bạn chọn được gồm 3 phần tử giống nhau dạng $\left\{ a,b,c \right\}$ có $C_{9}^{3}$ cách chọn.

TH2: Hai tập con các bạn chọn được gồm đúng 2 phần tử giống nhau dạng $\left\{ a,b,c \right\};\left\{ a,b,d \right\}$

+ Chọn ra hai phần tử $a,b$ có $C_{9}^{2}$ cách.

+ Chọn ra phần tử $c\in E\backslash \left\{ a,b \right\}$ có 7 cách.

+ Chọn ra phần tử $d\in E\backslash \left\{ a,b,c \right\}$ có 6 cách.

Trường hợp này có $C_{9}^{2}.7.6$ cách chọn. Vậy $n\left( A \right)=C_{9}^{3}+C_{9}^{2}.7.6.$ Xác suất cần tính bằng $\dfrac{C_{9}^{3}+C_{9}^{2}.7.6}{{{511}^{2}}}=\dfrac{228}{37303}.$

Các đề sưu tầm năm nay được Vted phát hành trong khoá Luyện đề Xplus

>>Xem thêm Cập nhật Đề thi thử tốt nghiệp THPT 2023 môn Toán có lời giải chi tiết

Combo 4 Khoá Luyện thi THPT Quốc Gia 2023 Môn Toán dành cho teen 2K5

Bộ Đề thi học sinh giỏi cấp tỉnh Môn Toán lớp 12 năm học 2022 – 2023 (Trắc nghiệm)

Đề thi học sinh giỏi cấp tỉnh Môn Toán lớp 12 năm học 2022 – 2023 sở GD&ĐT Phú Thọ

Đề thi học sinh giỏi cấp tỉnh Môn Toán lớp 12 năm học 2022 – 2023 sở GD&ĐT Bắc Ninh

Đề thi học sinh giỏi cấp tỉnh Môn Toán lớp 12 năm học 2022 – 2023 sở GD&ĐT Thanh Hoá

Đề thi học sinh giỏi cấp tỉnh Môn Toán lớp 12 năm học 2022 – 2023 sở GD&ĐT Thái Bình

Đề thi học sinh giỏi cấp tỉnh Môn Toán lớp 12 năm học 2022 – 2023 sở GD&ĐT Vĩnh Phúc

Đề thi học sinh giỏi cấp tỉnh Môn Toán lớp 12 năm học 2022 – 2023 sở GD&ĐT Nam Định